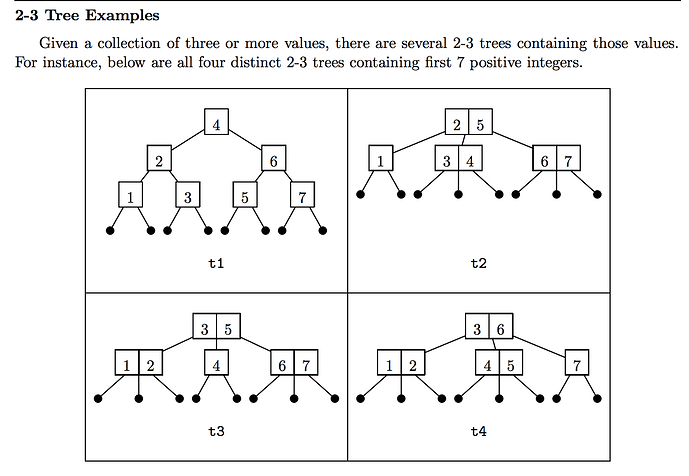
This is a Nim project but the idea is mainly in the scope of Clojure’s persistent data structure. I was alway curious about the details of persistent vectors. And thanks to the excellent post of Understanding Clojure’s Persistent Vectors, pt. 1 a lot of the details is revealed.
I was mostly using JavaScript and don’t have much experience in C or Java, so I choose Nim for my toy and Nim has comparable(kind of) performance to C. Nim has a builtin but optional GC, which makes my at ease.
Clojure is using a 32-branches tree for performance. I choose 3 for learning purposes. At first I thought a tree with 3 branches is more flexible for inserting, for example, it has both left and right, insertion could take place in both directions, and it’s more natural for tries to have left and right branches. Although it could be a not good choice for performance.
Luckily there are still some interesting things to be found in implementing such a data structure.
First, the list TernaryTreeList is implemented in a B+ tree, leaf nodes and internal nodes are different. Leaf nodes contains values, while internal nodes contains sizes of tree, and sizes are used as indexes. In Clojure Vectors, indexes are calculated like i >>> 5 to find each index in every level, that’s very fast. In TernaryTreeList, I have to comparing sizes of each branch from left to right to find out which branch contains the index I wanted, which has a cost in performance.
When a TernaryTreeList list is first initialized, values are distributed sparely but with a minimal depth. It’s not placed in a most compact way, just don’t be too deep. And that mean there will be some holes among the tree.
Concise notations
To show the structure in details, I would show a TernaryTreeList list, with 3 items, which means [1 2 3], structured like
^
/ | \
1 2 3
in a compact form:
(1 2 3)
if empty holes exist, that place would be left empty, which make [1 3] of:
^
/ | \
1 3
to be:
(1 _ 3)
and for deeper tree [1 4 5 6]:
^
/ | \
1 ^
/ | \
4 5 6
it becomes:
(1 _ (4 5 6))
thats much more concise.
Creating
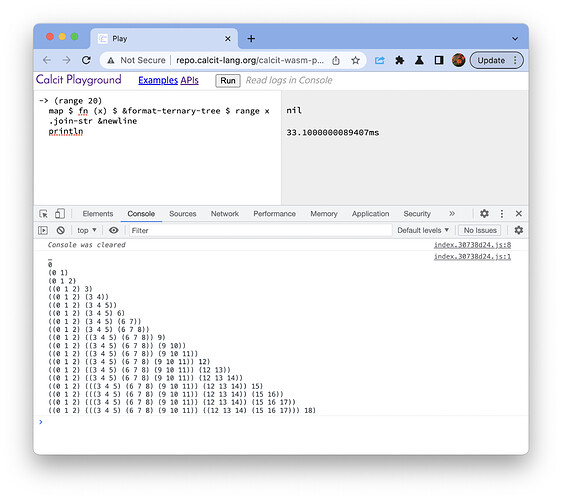
So when I init lists of ranges from 0 to 20, they are like:
(_ _ _)
1
(1 _ 2)
(1 2 3)
(1 (2 _ 3) 4)
((1 _ 2) 3 (4 _ 5))
((1 _ 2) (3 _ 4) (5 _ 6))
((1 _ 2) (3 4 5) (6 _ 7))
((1 2 3) (4 _ 5) (6 7 8))
((1 2 3) (4 5 6) (7 8 9))
((1 2 3) (4 (5 _ 6) 7) (8 9 10))
((1 (2 _ 3) 4) (5 6 7) (8 (9 _ 10) 11))
((1 (2 _ 3) 4) (5 (6 _ 7) 8) (9 (10 _ 11) 12))
((1 (2 _ 3) 4) ((5 _ 6) 7 (8 _ 9)) (10 (11 _ 12) 13))
(((1 _ 2) 3 (4 _ 5)) (6 (7 _ 8) 9) ((10 _ 11) 12 (13 _ 14)))
(((1 _ 2) 3 (4 _ 5)) ((6 _ 7) 8 (9 _ 10)) ((11 _ 12) 13 (14 _ 15)))
(((1 _ 2) 3 (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) 14 (15 _ 16)))
(((1 _ 2) (3 _ 4) (5 _ 6)) ((7 _ 8) 9 (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
(((1 _ 2) (3 _ 4) (5 _ 6)) ((7 _ 8) (9 _ 10) (11 _ 12)) ((13 _ 14) (15 _ 16) (17 _ 18)))
(((1 _ 2) (3 _ 4) (5 _ 6)) ((7 _ 8) (9 10 11) (12 _ 13)) ((14 _ 15) (16 _ 17) (18 _ 19)))
Since items are roughly equally distributed in 3 branches of each internal node, the holes are also sparsely distributed. It’s not a optimal solution because the overall depths of all items can still be reduced, and the existence of internals nodes also takes memory.
An alternative solution is giving the middle branch more items that is makes use of the full spaces of given depth, then the placement is compacter than above.
(_ _ _)
1
(1 _ 2)
(1 2 3)
((1 _ 2) 3 4)
((1 _ 2) 3 (4 _ 5))
((1 _ 2) (3 4 5) 6)
((1 _ 2) (3 4 5) (6 _ 7))
((1 2 3) (4 5 6) (7 _ 8))
((1 2 3) (4 5 6) (7 8 9))
(((1 _ 2) 3 4) (5 6 7) (8 9 10))
(((1 _ 2) 3 4) (5 6 7) ((8 _ 9) 10 11))
((1 _ 2) ((3 4 5) (6 7 8) (9 10 11)) 12)
((1 _ 2) ((3 4 5) (6 7 8) (9 10 11)) (12 _ 13))
((1 2 3) ((4 5 6) (7 8 9) (10 11 12)) (13 _ 14))
((1 2 3) ((4 5 6) (7 8 9) (10 11 12)) (13 14 15))
(((1 _ 2) 3 4) ((5 6 7) (8 9 10) (11 12 13)) (14 15 16))
(((1 _ 2) 3 4) ((5 6 7) (8 9 10) (11 12 13)) ((14 _ 15) 16 17))
(((1 _ 2) 3 (4 _ 5)) ((6 7 8) (9 10 11) (12 13 14)) ((15 _ 16) 17 18))
(((1 _ 2) 3 (4 _ 5)) ((6 7 8) (9 10 11) (12 13 14)) ((15 _ 16) 17 (18 _ 19)))
However to find the best-fit size. I have to divide size by 3 very frequently. That might be slower than dividing 2 in a binary computer…
Inserting
You may also wondering how it would be like if I keep appending elements at the end. This is how it looks like:
(_ _ _)
0
(0 1 _)
(0 1 2)
((0 1 2) 3 _)
((0 1 2) (3 4 _) _)
((0 1 2) (3 4 5) _)
((0 1 2) (3 4 5) 6)
((0 1 2) (3 4 5) (6 7 _))
((0 1 2) (3 4 5) (6 7 8))
(((0 1 2) (3 4 5) (6 7 8)) 9 _)
(((0 1 2) (3 4 5) (6 7 8)) (9 10 _) _)
(((0 1 2) (3 4 5) (6 7 8)) (9 10 11) _)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) 12 _) _)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) (12 13 _) _) _)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) (12 13 14) _) _)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) (12 13 14) 15) _)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) (12 13 14) (15 16 _)) _)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) (12 13 14) (15 16 17)) _)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) (12 13 14) (15 16 17)) 18)
(((0 1 2) (3 4 5) (6 7 8)) ((9 10 11) (12 13 14) (15 16 17)) (18 19 _))
It is quite compact. And take a looks a (range 10), which has 9 + 1 items:
(((0 1 2) (3 4 5) (6 7 8)) 9 _)
It’s consisted of 2 branches(and 1 extra empty branch) of 9 items and 1 elements. So accessing element 9 is quite fast since depth is 1, rather than go to look it up in a branch of a depth of 3.
How about prepending? It’s quite similar to appending:
(_ _ _)
0
(_ 1 0)
(2 1 0)
(_ 3 (2 1 0))
(_ (_ 4 3) (2 1 0))
(_ (5 4 3) (2 1 0))
(6 (5 4 3) (2 1 0))
((_ 7 6) (5 4 3) (2 1 0))
((8 7 6) (5 4 3) (2 1 0))
(_ 9 ((8 7 6) (5 4 3) (2 1 0)))
(_ (_ 10 9) ((8 7 6) (5 4 3) (2 1 0)))
(_ (11 10 9) ((8 7 6) (5 4 3) (2 1 0)))
(_ (_ 12 (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
(_ (_ (_ 13 12) (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
(_ (_ (14 13 12) (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
(_ (15 (14 13 12) (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
(_ ((_ 16 15) (14 13 12) (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
(_ ((17 16 15) (14 13 12) (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
(18 ((17 16 15) (14 13 12) (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
((_ 19 18) ((17 16 15) (14 13 12) (11 10 9)) ((8 7 6) (5 4 3) (2 1 0)))
Still take a look a (range 10), just a reverse structure:
(_ 9 ((8 7 6) (5 4 3) (2 1 0)))
It’s optimized on purpose since it’s quite common use case to add new items at head or at tail. The goal is too reduce holes inside the tree.
You may also curious how it looks like when items are inserted randomly, say using assocAfter, here’s how it appears(first integer indicates “depth”):
2 : (0 1 _)
2 : (0 1 2)
3 : ((0 3 _) 1 2)
3 : ((0 3 _) 1 (2 4 _))
4 : (((0 3 _) 1 (2 4 _)) 5 _)
4 : (((0 3 _) (1 6 _) (2 4 _)) 5 _)
4 : (((0 3 _) (1 6 7) (2 4 _)) 5 _)
4 : (((0 3 _) (1 6 7) (2 4 _)) (5 8 _) _)
5 : (((0 3 _) ((1 6 7) 9 _) (2 4 _)) (5 8 _) _)
6 : (((0 3 _) (((1 10 _) 6 7) 9 _) (2 4 _)) (5 8 _) _)
6 : (((0 3 11) (((1 10 _) 6 7) 9 _) (2 4 _)) (5 8 _) _)
6 : (((0 3 11) (((1 10 12) 6 7) 9 _) (2 4 _)) (5 8 _) _)
6 : (((0 3 11) (((1 10 12) 6 7) 9 _) (2 4 _)) (5 8 13) _)
6 : (((0 3 11) (((1 10 12) 6 7) 9 _) (2 4 14)) (5 8 13) _)
7 : (((0 3 11) ((((1 15 _) 10 12) 6 7) 9 _) (2 4 14)) (5 8 13) _)
7 : (((0 3 11) ((((1 15 _) 10 12) 6 7) 9 _) (2 4 14)) ((5 16 _) 8 13) _)
7 : (((0 3 11) ((((1 15 _) 10 12) 6 7) 9 _) (2 (4 17 _) 14)) ((5 16 _) 8 13) _)
7 : (((0 3 11) ((((1 15 _) 10 12) 6 7) 9 _) ((2 18 _) (4 17 _) 14)) ((5 16 _) 8 13) _)
7 : (((0 3 11) ((((1 15 _) 10 12) 6 (7 19 _)) 9 _) ((2 18 _) (4 17 _) 14)) ((5 16 _) 8 13) _)
7 : (((0 3 11) ((((1 15 _) 10 12) 6 (7 19 _)) 9 _) ((2 18 _) (4 17 20) 14)) ((5 16 _) 8 13) _)
; after balanced
4 : (((0 _ 3) (11 1 15) (10 _ 12)) ((6 _ 7) (19 9 2) (18 _ 4)) ((17 _ 20) (14 5 16) (8 _ 13)))
Sometimes it creates new branches, sometimes it fills in the holes. The depth grew quite fast into a depth of 7 since I wanted to share branches in most case. And larger depth means slower lookup and even more memory occupation.
To reduce depth, forceInplaceBalancing is called. The depth goes from 7 to 4. The count of holes and nodes are not necessarily reduced in current algorithm though…
You may also notice that it’s still reusing branches during random updates. Sister branches are reused, while parent branches are recreated.
Taking 13 for example, when it’s inserted, it’s at the tail, so the left branches are reused, only 2 new internal nodes are created, 7 internal nodes are reused.
6 : (((0 3 11) (((1 10 12) 6 7) 9 _) (2 4 _)) (5 8 _) _)
6 : (((0 3 11) (((1 10 12) 6 7) 9 _) (2 4 _)) (5 8 13) _)
And when 7 is inserted, 3 internal nodes are created, while 2 internal nodes are reused. This is not quite good though…
4 : (((0 3 _) (1 6 _) (2 4 _)) 5 _)
4 : (((0 3 _) (1 6 7) (2 4 _)) 5 _)
But if you take a balanced list and insert randomly, for example inserting 888 into (range 17) after each item:
4 : (((0 888 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 1 888) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 888 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 3 888) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 888 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
5 : ((((0 _ 1) (2 _ 3) (4 _ 5)) 888 _) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 888 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 7 888) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 888 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 9 888) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 888 11)) ((12 _ 13) (14 _ 15) (16 _ 17)))
5 : (((0 _ 1) (2 _ 3) (4 _ 5)) (((6 _ 7) (8 _ 9) (10 _ 11)) 888 _) ((12 _ 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 888 13) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 13 888) (14 _ 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 888 15) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 15 888) (16 _ 17)))
4 : (((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 888 17)))
5 : ((((0 _ 1) (2 _ 3) (4 _ 5)) ((6 _ 7) (8 _ 9) (10 _ 11)) ((12 _ 13) (14 _ 15) (16 _ 17))) 888 _)
Most times, only 2~3 new internal nodes are created among all 12~13 internal nodes, that’s not bad.
So the drawback is this tree does not balance automatically. During most of the lifetime of a list, it’s not balanced, so it would be not quite efficient. However I don’t a simple solution for that at current.
Concat and slice
Two other major operations on lists are slice and concat. If you don’t case about balancing, concat is fast, but increasing depth every time:
(1 (2 _ 3) 4) ; a
(5 (6 _ 7) 8) ; b
(9 (10 _ 11) 12) ; c
((1 (2 _ 3) 4) _ (5 (6 _ 7) 8)) ; a b
(((1 (2 _ 3) 4) _ (5 (6 _ 7) 8)) _ (9 (10 _ 11) 12)) ; a b c
it might trigger rebalancing at times though…
And for slicing, it still tries to reuse some branches but turned out not quite good… but it is supposed to be a little better if more items are sliced…
# part of nim code
for i in 0..<8:
for j in i..<9:
echo fmt"{i}-{j} ", d.slice(i, j).formatInline
; original structure
((1 2 3) (4 _ 5) (6 7 8))
0-0 (_ _ _)
0-1 1
0-2 (1 _ 2)
0-3 (1 2 3)
0-4 ((1 2 3) _ 4)
0-5 ((1 2 3) _ (4 _ 5))
0-6 (((1 2 3) _ (4 _ 5)) _ 6)
0-7 (((1 2 3) _ (4 _ 5)) _ (6 _ 7))
0-8 ((1 2 3) (4 _ 5) (6 7 8))
1-1 (_ _ _)
1-2 2
1-3 (2 _ 3)
1-4 ((2 _ 3) _ 4)
1-5 ((2 _ 3) _ (4 _ 5))
1-6 (((2 _ 3) _ (4 _ 5)) _ 6)
1-7 (((2 _ 3) _ (4 _ 5)) _ (6 _ 7))
1-8 (((2 _ 3) _ (4 _ 5)) _ (6 7 8))
2-2 (_ _ _)
2-3 3
2-4 (3 _ 4)
2-5 (3 _ (4 _ 5))
2-6 ((3 _ (4 _ 5)) _ 6)
2-7 ((3 _ (4 _ 5)) _ (6 _ 7))
2-8 ((3 _ (4 _ 5)) _ (6 7 8))
3-3 (_ _ _)
3-4 4
3-5 (4 _ 5)
3-6 ((4 _ 5) _ 6)
3-7 ((4 _ 5) _ (6 _ 7))
3-8 ((4 _ 5) _ (6 7 8))
4-4 (_ _ _)
4-5 5
4-6 (5 _ 6)
4-7 (5 _ (6 _ 7))
4-8 (5 _ (6 7 8))
5-5 (_ _ _)
5-6 6
5-7 (6 _ 7)
5-8 (6 7 8)
6-6 (_ _ _)
6-7 7
6-8 (7 _ 8)
7-7 (_ _ _)
7-8 8
Others
I also did some experiments on persistent map with ternary tree. It’s using a trie but the hashes(which are integers) are used for indexing, and lookup steps are similar. Maps could be a lot deeper since hashes are really sparse. I could perform forced balancing as well but it’s always a lot deeper than lists. No much experience yet…
I’ve using this library in my other toy projects for a while. Some optimizations is added and it should not be very slow now. Anyway it’s quite interesting journey to play with a similar tree structure like the persistent data structure I used for years in Clojure.
Advices on optimizations are welcome. (not going to switching from ternary
branches in this project though…)